Matematik med frisbee
Spil og regn med frisbee og kast. To forskellige spil, der lægger op til frisbeematematik.

Kort beskrivelse
Aktiviteten er tilrettelagt til 24 elever, der deles op i to grupper:
-
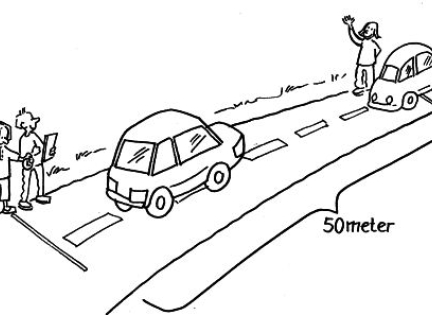
Tættest på pinden: To hold á 6 elever kaster frisbees efter en pind og måler afstanden.
- Frisbee-golf: En gruppe på 12 elever går sammen to og to og spille discgolf på en 6 ”hullers” bane.
Efterfølgende behandler eleverne deres resultater i klassen. De arbejder med omskrivning af længdemål, gennemsnit, forskel, sum, centicubes og lommeregneren.
Formål
Eleverne arbejder i grupper med kast, opmåling af afstand, beregning af point og gennensnit, addition, subtraktion, multiplikation og division. De fører deres resultater ind i tabeller og diagrammer og diskuterer dem med klassen.
Forberedelse
Sæt dig ind i de to spil, "Frisbee-golf" og "Tættest på pinden". Du må selv lave arbejdsark ud fra de ideer der er foreslået nedenfor.
Sådan gør du
Her er de to spil.
Frisbee-golf
Regler
En gruppe på 12 elever laver en 6 ”hullers” bane med afstande på 20-40 m mellem keglerne. Banen kan startes og afsluttes ved samme kegle. Således skal man bruge 6 kegler. Eleverne går sammen om en frisbee 2 og 2 så der bliver 6 hold. Deltagerne på de enkelte hold skiftes til at kaste og antallet af kast på hvert enkelt ”hul” noteres på scorekortet (se nedenfor + kopiark). Frisbeen er først i hul, når keglen rammes.
Eleverne beregner point ved at trække antallet af kast fra 7 på scorekortet. Hvis skal bruge 7 eller flere kast, får man 0 point.
Husk det hele tiden er holdet fjernest fra pinden der kaster.
Scorekort til frisbee-golf
Navn: ___________________ Klasse: ___________________ Dato: _________
|
Hul
|
Kast
|
Point
|
|
1
|
|
|
|
2
|
|
|
|
3
|
|
|
|
4
|
|
|
|
5
|
|
|
|
6
|
|
|
|
I alt
|
|
|
Resultatliste til frisbee-golf
Stil jeres resultater op i en resultatliste - og svar på spørgsmålene nedenfor.
| Nummer | Navn | Point |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
| 5 | ||
| 6 |
Opgaver:
- Hvilket hold fik flest point? ______
- Hvor stor er pointforskellen på nummer 1 og nummer 3 ? _______
- Hvor stor er pointforskellen på nummer 2 og nummer 4 ? _______
- Hvor stor er pointforskellen på nummer 5 og nummer 6 ? _______
- Hvor mange point fik alle hold tilsammen ? ________
- Hvor mange point fik holdene i gennemsnit ? _______
Arbejdsark til frisbee-golf
|
11
|
|
|
|
|
|
|
|
10
|
|
|
|
|
|
|
|
9
|
|
|
|
|
|
|
|
8
|
|
|
|
|
|
|
|
7
|
|
|
|
|
|
|
|
6
|
|
|
|
|
|
|
|
5
|
|
|
|
|
|
|
|
4
|
|
|
|
|
|
|
|
3
|
|
|
|
|
|
|
|
2
|
|
|
|
|
|
|
|
1
|
|
|
|
|
|
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
Opgaver:
Brug først centicubes til at finde gennemsnit for dine kast. Brug så lommeregneren til at se, hvor tæt du kom på. Husk at skrive regnestykket op, så du kan huske hvad du har tænkt.
1) Hul 1 og 2 _______________
Lommeregner: ______________
Lommeregner: ______________
2) Hul 2 og 3 _______________
Lommeregner: ______________
3) Hul 3 og 4 _______________
Lommeregner: ______________
4) Hul 4 og 5 _______________
Lommeregner: ______________
5) Hul 5 og 6 _______________
Lommeregner: ______________
6) Hul 1, 2 og 3 _____________
Lommeregner: ______________
7) Hul 1, 3 og 4 ______________
Lommeregner: ______________
8) Hul 2, 3 og 5 ______________
Lommeregner: ______________
9) Hul 4, 5 og 6 _______________
Lommeregner: _______________
Lommeregner: _______________
10) Alle hullerne ______________
Lommeregner: _______________
Lommeregner: _______________
Tættest på pinden
En anden gruppe på 12 elever kaster frisbees mod en pind.
- Seks elever stiller op på en række og kaster en ad gangen.
- De andre elever måler afstande og fører dem ind i skemaet nedenfor.
- Så byttes rollerne om.
- Når alle deltagere har kastet 3 gange og alle resultater er noteret i skemaet, er aktiviteten slut og eleverne går videre til frisbeegolf, hvor de skal samle kegler ind undervejs.
Resultatark for tættest på pinden
Fyld skemaet ud med alles navne. Skriv afstand fra frisbee til pind for første, andet og tredje kast. Læg de tre kast sammen og skriv resultatet i skemaet.
|
Navn
|
1. kast
|
2. kast
|
3. kast
|
Afstand i alt
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Opgaver:
1) Hvilket enkelt kast var tættest på pinden ?
Navn: ________________
Afstand: _____________
Afstand: _____________
2) Hvilket enkelt kast var længst fra pinden ?
Navn: ________________
Afstand: _____________
Afstand: _____________
3) Hvad blev gennemsnittet af dine 3 kast (skriv også regnestykket)
___________________________________________
Vinderskamlen for tættest på pinden
Find første, anden og trediepladsen og udfyld dette skema. (Den mindste afstand har vundet.)
|
Nummer
|
Navn
|
m og cm
|
cm
|
m
|
|
1
|
|
|
|
|
|
2
|
|
|
|
|
|
3
|
|
|
|
|
Bearbejdning
Efterfølgende behandler eleverne deres resultater i klassen. De arbejder med omskrivning af længdemål, gennemsnit, forskel, sum, hovedregning, centicubes og lommeregner.
Baggrund
Udeskolebånd i Lemvig kommune
Dette materiale er lavet af lærere i Lemvig kommune. Dansk og matematiklærere fra alle kommunens 4. klasser har i efteråret 2009 arbejdet med at kvalificere ”Udeskoleaktiviteter” fagligt gennem kursusforløb, fælles udvikling og egne erfaringer.
Ud af dette forløb kom der mange aktiviteter og undervisningsforløb, der her er beskrevet og kan anvendes af alle, der har lyst til selv at arbejde ude.
Forløbene er planlagt, udviklet og gennemført, hvorefter de er evalueret gennem sparring og beskrevet detaljeret. Forløbene er samlet og redigeret af lektor Karen Barfod, FleXika og læreruddannelsen i Nørre Nissum.
Udeskole er en skoleform, hvor børnene undervises regelmæssigt uden for skolens mure i folkeskolens almindelige fag. Denne måde at undervise på har vist sig at give en mere helhedsorienteret og dyb læring, hvor børnene arbejder med hele kroppen, sanserne og hovedet i en integreret læringsproces. I Lemvig Kommune satses der på, at alle 4. klasser kommer til at arbejde med udeskoleaktiviteter.
I dette kursusforløb er der arbejdet med fagene Dansk og Matematik, men også med andre fag, både enestående og på kryds og tværs. Materialet her afspejler den store mangfoldighed og de mange muligheder, udeskoleaktiviteterne åbner for børn og deres lærere.
God fornøjelse og god arbejdslyst – det er ikke kun en ny måde at lære på, det er også en ny måde at være lærer på!