Snoren rundt om jorden

Kort om forløbet
Tit bruger vi vores intuition eller snusfornuft til at løse matematiske problemer. Den giver som regel gode resultater. Men den kan også nogle gange snyde. Denne opgave handler om at sammenligne det, resultat vi tror vi får, med det resultat, vi rent faktisk får – og undersøge, om vores snusfornuft snyder os.
Formål
Formålet er at lære cirklens geometri at kende.
Forberedelse
Hvis klassen i forvejen arbejder med geometri – og særligt cirklens geometri og omkreds – er det oplagt at gå ud og lave denne aktivitet.
Find et sted med cirkler
I skal arbejde ude et sted, hvor der findes cirkulære former af forskellig størrelse. Det kan være en cylindrisk affaldsbeholder, en cykel som man kan lægge ned, en karrusel på en legeplads, cirkulært kloakdæksel, et cirkulært rør til et skilt, en medbragt tallerken, en cirkulær stolpe til et gyngestativ, lygtepæle, gylletanke, brandhaner, tallerkner, grydelåg, øldåser, bildæk, osv.
Vigtigt er, at der kan lægges en snor om den cirkulære form på jorden.
Elever i par
Del klassen op i grupper af to personer. Den ene elev har en rulle snor og en saks, den anden har en målestok.
Sådan gør du
Opgaven er formuleret til eleverne nedenfor.
Første opgave
Find den største cirkulære genstand i området. Det kan eksempelvis være et kloak-dæksel som vist på tegningen ovenfor.
Læg snoren ud langs kloak-dækslets omkreds indtil snoren møder snor-enden. Klem med to fingre på snoren på det sted, hvor den møder snor-enden – og mål herfra endnu en meter til klippepunktet.

Klip snoren over i klippepunktet, så du har en snor, som er lig med omkredsen af den kloak-dækslet plus en meter (se tegning 2).
Læg nu snoren i en cirkel rundt om kloak-dækslet, så snor-enderne støder sammen – og så snorens cirkel hele tiden har den samme afstand til kloak-dækslet (se tegning 3).

Når du mener, at snoren ligger rigtigt, skal du måle afstanden mellem omkredsen af kloak-dækslet og snorens cirkel.
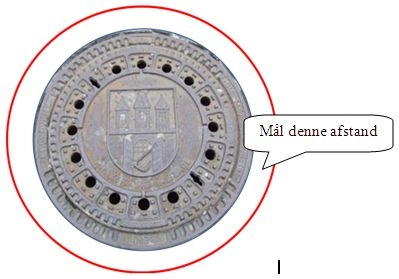
Skriv afstanden op på dit papir.
Anden opgave
Vælg nu en anden cirkulær genstand. Inden du går i gang med den samme slags måling, skal du gætte på, hvad resultatet bliver – dvs. hvad bliver afstanden mellem genstandens omkreds og snorens cirkel, når du igen forlænger snoren med en meter.
Skriv dit gæt op
Læg nu igen snoren ud langs den cirkulære genstands omkreds indtil snoren møder snor-enden. Klem med to fingre på snoren på det sted, hvor den møder snor-enden – og mål herfra en meter til klippepunktet.
Klip snoren over i klippepunktet, så du har en snor, som er lig med omkredsen af den cirkulære genstand plus en meter (se tegning 2).
Herefter skal du lægge snoren i en cirkel rundt om den cirkulære genstand, så snor-enderne støder sammen – og så snorens cirkel hele tiden har den samme afstand til den cirkulære genstand (se tegning 3).
Når du mener, at snoren ligger rigtigt, skal du måle afstanden mellem omkredsen af den cirkulære genstand og snorens cirkel.
Skriv den målte afstand op.
Fik du det samme resultat, som du gættede på. Hvorfor? Hvorfor ikke?
Tredje opgave
Den tredje opgave er som de to foregående.Den eneste forskel er, at du som udgangspunkt vælger en tredje cirkulær genstand.
Igen skal du gætte resultatet, før du går i gang med at rulle snor ud, forlænge snor og lægge snor i en cirkel for til sidste at måle afstanden mellem omkredsen af den cirkulære genstand og snorens cirkel.
Fik du det resultat, du gættede på? Hvorfor? Hvorfor ikke?
Fjerde opgave
Her skal du ikke måle. Du skal sammenligne dine måleresultater.
Du har brugt tre forskellige cirkulære genstande som udgangspunkt for dine opgaver. De havde tre forskellige størrelser.
Hvad med dine målte afstande – gav de også tre forskellige tal?
Hvis du nu tænker på usikkerheden ved dine målinger, fik du så i grunden tre forskellige tal?
Femte opgave
Denne opgave er en beregningsopgave, fordi du ikke kan udføre den i praksis.
Opgaven handler om at trække en snor rundt om hele jordkloden – og derefter lægge en meter til længden af snoren.
Du skal beregne hvor højt denne ”snor-cirkel” ville hæve sig over jorden (hvis nu jorden også var cirkelrund). Gæt først på et tal, inden du går i gang.
Dernæst skal du have lidt hjælp:
- Jordens omkreds er 40.000 km
- Jordens radius er 6357 km
Sjette opgave
Som afsluttende opgave skal du forklare – evt. ved at opstille en ligning for dine beregninger – hvordan det kan være, at du får de pågældende resultater i de foregående opgaver.
Kan det forklares, hvorfor der er en sammenhæng mellem resultatet i forbindelse med jorden som cirkulær genstand og de andre cirkulære genstande?
Her er starten på ligningen:
π (pi) = 3,1416
Omkredsen af jorden er 2 π R
Omkredsen af snor-cirklen er 2 π R + 1
Radius i snor-cirklen er R + x
Omkredsen af snor-cirklen kan derfor også skrives 2 π (R + x)
Ved at sige, at de to udtryk for omkredsen er ens fås:
2 π R + 1 = 2 π (R + x)
Hvad kan du nu sige om værdien af x?
Baggrund
Definitionen på en cirkel
Hvis du binder en sten i en snor og svinger den rundt, laver du en cirkel. Denne lille leg indeholder faktisk definitionen på en cirkel – alle de punkter som i et plan ligger lige langt fra et bestemt punkt (centrum).
Cirkel som inspiration
Cirklen er en geometrisk figur. Den har altid fascineret kunstnere, videnskabsfolk og håndværkere:
- Cirklen er grundlaget for hjulet, som er én af de største opfindelser i menneskehedens historie
- Drejeskiven har i århunreder gjort os i stand til at skabe krukker og runde fade til opbevaring af fødevarer
- Arkitekter og havekunstnere har altid været optaget af at bruge cirklen som dekoration
- Stjernernes bevægelser blev tidligere beskrevet ud fra cirkelbevægelser – ikke blot pga. af astronomernes iagttagelser, men også, fordi cirklen var den mest perfekte figur,- og da stjernerne er nærmest Gud, ligner de Gud mest, derfor bevæger de sig i cirkler (først med de moderne astronomer blev denne argumentation forkastet).