Primitive kastemaskiner
Byg primitive kastemaskiner og fyr den af i fysik! Forløbets grundide kan også bruges i natur/teknologi.
Kort om forløbet
Elevernes opgave er at designe og bygge en affyringsmekanisme, der kan kaste eller skyde en tennisbold så langt som muligt, med størst mulig præcision - og samtidig være flytbar. Til denne opgave kan eleverne bruge brædder og andre materialer de får udleveret, samt det de selv kan finde omkring sig i naturen eller bygninger.
Formål
- Eleverne skal aktivt bruge matematikkens og fysikkens principper i konstruktion af kastemaskiner
- Eleverne skal kende til trekantsprincippet og kunne bruge det i konstruktion
- Eleverne skal kende til og arbejde med overførsel af kræfter i kastemaskiner
- Eleverne skal kende til og arbejde med materialers forskellige egenskaber
-
Eleverne skal kunne vurdere og sammenligne forskellige kastemaskiner, og begrunde hvorfor nogle skyder længere, mere nøjagtigt og er mere holdbare end andre.
Forberedelse
Forsøget her kan sagtens afvikles for sig selv, men det kan også suppleres af to forsøg, som vil være gode at starte med. Du kan finde de to forsøg i afsnittet "Ekstra forsøg og opgaver" nedenfor.
Forberedelse i klassen
A: Indføring i kastemaskiner og deres forskellige mekanismer
-
Søg på www.youtube.com på: ”kastemaskiner”,”trebuchet”, ”katapult”.
- Brug billedsøg på www.google.com søg på: ”kastemaskiner”,”trebuchet”, ”katapult” ◦ Brug dette som udgangspunkt for en samtale med eleverne, hvor I afdækker forskellige affyringsmekanismer, krafoverføringsprincipper, og låsemekanismer
B: Indføring i konstruktion:
I forløbet her skal I bygge kastemaskiner, som er stærke og står stabilt. Brug derfor trekantsprincippet i jeres konstruktioner - og introducer det for eleverne i klassen.
-
TrekantsprincippetHvis man gerne vil have en stærk konstruktion, som kun vejer lidt, så er trekanten ideel.
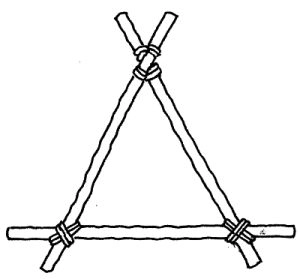Her er en A-buk af rafter, som spejderne bruger, i deres ofte høje og stærke pioner-konstruktioner.Tegning: Eva Wulff.
Det princip har mennesker til alle tider brugt, når vi bygger huse. Kig op og se på tagkonstruktionerne. Rigtig mange er trekantede og har det man kalder gitterspær – dvs. en stor trekant, som er delt op i mindre trekanter.
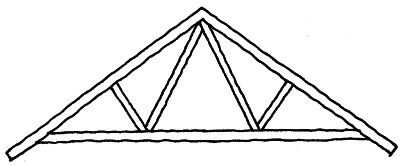Gitterspær i tage er trekantede - og delt op i flere trekanter for at give større styrke.Tegning: Eva Wulff.
Tænk også på et gammeldags telt. To teltstænger, som holdes oprette af teltdug og barduner i – ja trekanter.Også i brokonstruktioner arbejder ingeniørerne med trekanter – tænk f.eks. på den gamle lillebæltsbro.
Hvis en firkant skal gøres stabil, så kan man dele den i to trekanter med en ekstra stang diagonalt – eller i fire via to diagonaler. Hvis I kigger på gamle bindingsværkshuse, kan I også se, at grundkonstruktionen godt kan være firkantet – men ude i hjørnerne, hvor huset skal være ekstra stærkt, er der sat skråstivere ind.
Forberedelse ude
- Alt materialet skal fragtes til byggestedet. Det kan eleverne hjælpe med.
Konstruktion og udvikling af kastemaskine.
Foto: Martin V. Juhler.
Sådan gør du
Konstruktion
Elevernes opgave er at designe en affyringsmekanisme, der kan kaste eller skyde en tennisbold så langt som muligt, med størst mulig præcision, og samtidig være stærk og flytbar. Arbejdet foregår i grupper af fire elever. Hvis der bliver flere, er det svært for alle eleverne at komme til at indgå i konstruktionssamarbejdet.
Eleverne får udleveret materialer til at bygge kastemaskinen - og må også bruge materialer de kan finde i natur og bygninger omkring jer.
En kastemaskine.
Foto: Martin V. Juhler.
Konkurrencen om bedste konstruktion
Grupperne konkurrerer i disse tre discipliner:
-
Distance: Hvilket hold kan kaste bolden længst med tre kast?
-
Præcision: Hvilket hold kan rammer tættest på et givent mål?
-
Konstruktion: Hvilke konstruktionstekninikker er brugt? Hvorfor? Hvordan er holdbarhed, affyringsmekanisme, kastemekanisme, vægt? Ved diskussion findes den bedste konstruktion, som præmieres.
Stærk og let konstruktion. Den lange arm vipper over et punkt. Cykelslange danner det elastiske element.
Foto: Martin V. Juhler.
Dokumentation under og efter konstruktion
-
Eleverne skal løbende tage billeder under konstruktionsprocessen.
-
Eleverne skal tage 360 graders slutbilleder.
-
Eleverne skal optage video af kastemaskinen i funktion, set fra siden, således at hele kastet kan ses. Sørg for at videoen dokumenterer længden af de forskellige kast.
Bearbejdning
Fysik/kemi: Kastemaskiner, design og udførsel, hvad skete og hvorfor?
Tag udgangspunkt i de videosekvenser og billeder, som eleverne har taget af deres kastemaskiner:
- Find kastevinkel se "Vinkelmåling i windows paint og vinkelmåling på smartboard"
-
Hvilken vinkel giver det længste kast, og hvorfor?
-
- Find hastigheden af kastene (aflæs starttid og sluttid på videoen, divider med længden)
-
Er det tennisboldens reelle hastighed?
-
-
Hvilke kraftoverførsler, potentiel og kinetisk, sker der før, under og efter affyring, i elevernes egne kastemaskiner?
-
Hvordan omsættes energien i de forskellige kastemaskiner?
-
Hvad kunne have gjort at kastemaskinerne havde skudt længere?
Matematik: Eleverne og deres egne kastemaskiner
Tag udgangspunkt i de videosekvenser og billeder som eleverne har taget af deres kastemaskiner.
-
Beregn de forskellige vinkler, der er i elevernes konstruktion - lever dette op til trekantsprincippet? Brug paint/smartboard se "Vinkelmåling i windows paint og vinkelmåling på smartboard".
-
Se på designet
-
Hvorfor er der nogle konstruktioner der holder bedre end andre?
-
Har eleverne levet op til trekantsprincippet
-
Ekstra forsøg og opgaver
Ekstra forsøg og opgaver, som I med fordel kan arbejde med, før I bygger kastemaskiner.
A: Den perfekte kastevinkel
Dette er en mulig måde at undersøge eksperimentelt, hvilken vinkel der giver det længste skud, da matematikken bag fænomenet er for avanceret for 7-10 klasse.
Konstruer et apparat til at måle kastevinkel.
Foto: Martin V. Juhler.
-
Cylinderen består af et nedløbsrør i aluminium, som jeg har sat en bund i. Røret er fastgjort med et spændebånd, der på bagsiden bliver strammet med en vingemøtrik.
-
En gevindstang går inde i røret. I den ene ende er der et håndtag og i den anden en plade der er lidt mindre end rørets diamenter - begge fastgjort med 2 bolte.
-
Midten af stangen er glatslebet, og en rimelig stiv fjeder på 15 cm er sat på.
- En plade er skåret ud som en vinkelmåler. Den har fået fræset en rille, så vinklen kan ændres, og har fået påtegnet vinkelmål langs kanten.
|
Elevopgave 1: Den perfekte kastevinkel
Ved hvilken vinkel tror I at tennisbolden kommer til at flyve længst, hvorfor?
Hastighed = Længde/tid
Hastighed = __________ m/sek Hastighed = ___________ km/time
|
B: Affyringsmåder og materialeegenskaber
Det er vigtigt at få eleverne til at tænke over materiale og deres egenskaber i forhold til forskellige måder at designe affyringsmekanismer på. Det kan man gøre, ved at bygge de to nedenstående kastemaskiner. Dimensionen kan varieres med disse er B: 50 cm x L:75 cm x ca. H: 100 cm, hvilket gør dem lette at transportere i en almindelig bil - og samtidig store nok til, at de holder til elevernes brug.
- Kastemaskine 1 oplagre potentiel energi, ved at man spænder siderne af kastemaskinen ind. Derfor vil det materiale, der strækker sig mindst, give det længste skud.
Kastemaskine 1.
Fotos: Martin V. Juhler.
-
Kastemaskine 2 oplagre potentiel energi ved forstrækning af materialet. Derfor vil det materiale, der kan strækkes længst og har hurtigst mulig sammentrækning, give det længste kast.
Kastemaskine 2.
Fotos: Martin V. Juhler.
|
Elevopgave 2: Affyringsmåder og materialeegenskaber
Hovedopgave:
Hvilken af de to kastemaskiner foran jer tror i kommer til at skyde længst, og hvorfor?
_______________________________________________________________
_______________________________________________________________
_______________________________________________________________
Til hver af kastemaskinerne stilles disse to spørgsmål:
Før afprøvning:
Hvilke af de tre materialer, cykelslange, baggagestrop og fladt nylonbånd, vil give det længste skud? _________________________________________________________
Hvorfor mener I det? ____________________________________________
Efter afprøvning:
Hvilke af de 3 materialer, cykelslange, baggagestrop og fladt nylonbånd, gav det længste skud?
______________________________________________________________
Hvorfor tror I at det var det materiale der gjorde det?___________________
Efter forsøg med de to kastemaskiner:
Hvilken af de to kastemaskiner skød længst, og hvorfor tror I at den gjorde det?
________________________________________________________________
________________________________________________________________
________________________________________________________________
|
Baggrund
Master
Udviklingen af dette undervisningsforløb er sket i sammenhæng med min masteropgave "Ud med skolen - undersøgelse på udeundervisning i matematik og fysik", og jeg vil her gøre rede for nogle af de hovedtanker jeg har gjort mig under udvikling af det aktivitetsbaserede udeundervisningsmateriale til matematik- og fysikundervisningen.
Sammenhæng mellem inde og ude
Udeundervisningsforløbet skal have en sammenhæng før, under og efter forløbet med både fysik- og matematikundervisningen. Derfor tager forløbet udgangspunkt i både Fælles Mål og kompetencemålene med det formål at underbygge og anvende disse. Samtidig har både lærer og elever mulighed for at indsamle notater, billeder og video fra udeundervisningsdagen, til en portefolie til de enkelte elever samt til klassen.
Til læreren lavet et oplæg både til viderearbejde og efterbearbejdning, hvor eleverne udforsker de emner de har arbejdet med på udeundervisningsdagen. På den måde får udeundervisningsdagen en tæt sammenhæng med den almindelige undervisning og den læring, der sker her, således at vi undgår at udeundervisningsoplæget for karakter af en happening. Samtidig skaber udeundervisningsdagen primært fælles erfaringer inden for klassen omkring emnet, hvilket giver et fælles udgangspunkt, som med fordel kan benyttes i det videre arbejde.
Tilbagetrukket stillads
Rollen som underviser under forløbet er tænkt anderledes end den meget lærercentrerede, som ofte bruges i klasseværelset. Under afviklingen af forløbet skal lærerens rolle være minimal, så det bliver eleverne og deres arbejde, der kommer i centrum.
Når læreren nedtoner sin rolle og gør klart, at eleverne selv skal finde løsningen på opgaven, får eleverne mulighed for selv at tænke, eksperimentere, og komme frem til løsninger på de opgaver, som de bliver stillet overfor. Læreren skal opfatte sig selv mere som et hjælpende stillads for eleverne, ved at stille spørgsmål, så eleverne selv kommer til at se og forholde sig til de forskellige problemstillinger, der vil dukke op under deres arbejde.
Udgangspunktet for forløbene er konstruktivismen som teoriramme. Denne tager udgangspunkt i de enkelte elever og hvordan de lærer, men er i sig selv ikke en arbejdsmetode. Konstruktivismen danner i midlertidigt en konstruktionsramme, hvilken jeg har brugt som grundlag under udvikling af de aktivitetsbaserede udeundervisningsforløb. Ud fra denne tanke skulle den aktivitetsbaserede udeundervisning gerne fordre:
-
en åben opgavestruktur hvor initiativ, aktivitet, problemløsning, eksperimentring, det virkelighedsnære, mening og medansvar er i fokus.
-
at eleverne bliver aktive medspillere og dermed engagerede og motiverede.
-
en induktiv tilgang til arbejdet.
-
at elevernes arbejde bliver centralt og bærende.
-
en proces der udfordrer og benytter begge hjernehalvdele.
-
at eleverne danner sig nye erfaringer på baggrund af arbejdet med projektet.
