Fra kort til virkelighed
Problemregning i virkeligheden. Brug geometri til at afmærke et punkt, du ikke kan se.

Kort om forløbet
Problemregning i virkeligheden. Ved hjælp af en kompasretning, en meterstok og et tov med 12 knuder skal eleverne afmærke et punkt, som de ikke kan se, på den anden side af et hus.
Formål
- Eleverne skal lære at bruge matematikken aktivt, som grundlag for at løse problemstillinger
- Eleverne skal konstruere retvinklede trekanter via tov, og anvende 3-4-5 regelen
- Eleverne skal bruge et parallelogram og reglerne for dette for at komme rundt om en forhindring
-
Eleverne skal bruge kompas, og dettes inddeling i grader, for at kunne udlægge vinkler.
Forberedelse
Sæt opgaven op ude
-
Find først et passende sted for opgaven. Du skal bruge et hushjørne, som du ser det på tegningen øverst i forløbet.
-
Afmærk et startpunkt foran hushjørnet og en kompasretning, som går ind igennem huset.
-
Konstruer opgaven, så du giver eleverne kompasretningen og en afstand fra start til slut. Elevernes opgave er, at markere et slutpunkt på den anden side af huset så præcist som muligt, uden andre hjælpemidler end et kompas, et stykke tov, en meterstok og en skriveblok.
-
Benyt selv løsningsforslaget nedenfor til at markere slutpunktet (se også kopiark i højre margin).
- Tegn et stort koordinatsystem med malertape på en pressening. Marker med tal langs x-aksen og med bogstaver langs y-aksen. Læg presseningen ud ved dit slutpunkt - sæt den evt. fast med pløkke - og noter i hvilket punkt slutpunktet befinder sig.

Mål den parallelle afstand ud ved at bruge rette vinkler.
Grafik: Martin V. Juhler.
Forberedelse i klassen
Opgaven er åben, men for at kunne gennemføre den, skal eleverne kunne lave en ret vinkel uden vinkelmåler - og kunne forstå og bruge et kompas. Det skal de lære i klassen.
At lave en ret vinkel uden vinkelmåler
I det gamle Ægypten brugte man en enkel metode, når man skulle bruge en ret vinkel. Ægypterne brugte et tov med 12 knuder, der har samme indbyrdes afstand, og lagde tovet som vist på tegningen. Denne måde at konstruere en retvinklet trekant på er også kendt som 3-4-5 reglen.
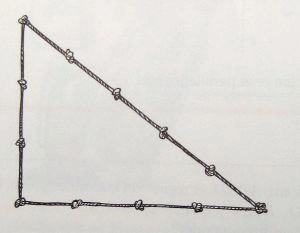
3-4-5 reglen. Mål en ret vinkel ud vha et tov med 12 knuder. Hvis trekanten er retvinklet, vil en side være 3, en side være 4 og hypotenusen være 5.
Indstil et kompas
- Vis eleverne, hvordan et kompas er opbygget.
- Vis eleverne, hvordan man indstiller kompassets retning til et givent antal grader.
- Vis eleverne, hvordan man orienterer kompasset, når et antal grader er indstillet.
Sådan gør du
-
Del eleverne op i grupper af 4-5 personer.
-
Giv eleverne opgaven som kopiari (se i højre margin)
- Sørg for, at eleverne har forstået opgaven
- Forhold dig passiv/støttende stilladserende under elevarbejdet
- For læreren er opgaven løst som skitseret i løsningsforslaget (se tegning ovenfor og kopiark. Men den kan også løses på andre måder.
Opgave: Find og marker punktet
I står ved startpunktet. I skal markere slutpunktet som ligger __________ meter ude med kompasretningen _______ så nøjagtigt som muligt. I har kun et tov med 12 knuder, en meterstok, et kompas og skriveblok og blyant til jeres rådighed.
I står ved startpunktet. I skal markere slutpunktet som ligger __________ meter ude med kompasretningen _______ så nøjagtigt som muligt. I har kun et tov med 12 knuder, en meterstok, et kompas og skriveblok og blyant til jeres rådighed.
Når I har fundet slutpunktet, skal I lægge en sten på punktet. Tag billeder af, hvor dette punkt er, således at man kan se jeres placering i forhold til kordinatsystemet på jorden.
Bearbejdning
I felten og i klassen
1) Tal med eleverne om, hvad de tænkte, da de skulle løse opgaven
- Ligheder og forskelle eleverne i mellem
2) Tydeliggør for eleverne, hvordan de har brugt matematik til at løse opgaven.
- Konstruktion af rette vinkler
- Brug af kompas
-
Parallelogram og regler for denne
Ekstra opgave til 3-4-5 reglen
Pythagoras – og reglen for retvinklede trekanter:
- Hvor mange ruder er der i det største kvadrat?
- Hvor mange ruder er der i de to mindste tilsammen?
-
Hvilken regel ser ud til at gælde?
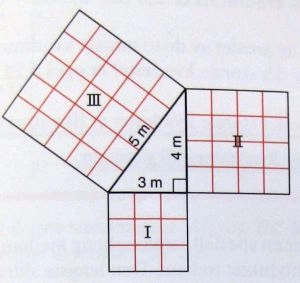
Alternativ opgave
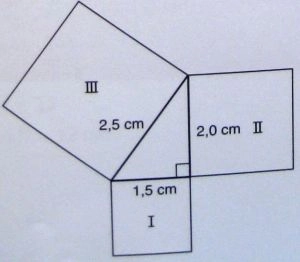
- Tegn en retvinklet trekant med siderne 1,5 cm, 2 cm og 2,5 cm.
- Tegn kvadrater på hvert af den retvinklede trekants sider
- Udregn arealet af de 3 kvadrater
-
Hvor stort er arealet af det største kvadrat i forhold til de to mindste?
Baggrund
Master
Udviklingen af dette undervisningsforløb er sket i sammenhæng med min masteropgave "Ud med skolen - undersøgelse på udeundervisning i matematik og fysik", og jeg vil her gøre rede for nogle af de hovedtanker jeg har gjort mig under udvikling af det aktivitetsbaserede udeundervisningsmateriale til matematik- og fysikundervisningen.
Sammenhæng mellem inde og ude
Udeundervisningsforløbet skal have en sammenhæng før, under og efter forløbet med både fysik- og matematikundervisningen. Derfor tager forløbet udgangspunkt i både Fælles Mål og kompetencemålene med det formål at underbygge og anvende disse. Samtidig har både lærer og elever mulighed for at indsamle notater, billeder og video fra udeundervisningsdagen, til en portefolie til de enkelte elever samt til klassen.
Til læreren lavet et oplæg både til viderearbejde og efterbearbejdning, hvor eleverne udforsker de emner de har arbejdet med på udeundervisningsdagen. På den måde får udeundervisningsdagen en tæt sammenhæng med den almindelige undervisning og den læring, der sker her, således at vi undgår at udeundervisningsoplæget for karakter af en happening. Samtidig skaber udeundervisningsdagen primært fælles erfaringer inden for klassen omkring emnet, hvilket giver et fælles udgangspunkt, som med fordel kan benyttes i det videre arbejde.
Tilbagetrukket stillads
Rollen som underviser under forløbet er tænkt anderledes end den meget lærercentrerede, som ofte bruges i klasseværelset. Under afviklingen af forløbet skal lærerens rolle være minimal, så det bliver eleverne og deres arbejde, der kommer i centrum.
Når læreren nedtoner sin rolle og gør klart, at eleverne selv skal finde løsningen på opgaven, får eleverne mulighed for selv at tænke, eksperimentere, og komme frem til løsninger på de opgaver, som de bliver stillet overfor. Læreren skal opfatte sig selv mere som et hjælpende stillads for eleverne, ved at stille spørgsmål, så eleverne selv kommer til at se og forholde sig til de forskellige problemstillinger, der vil dukke op under deres arbejde.
Udgangspunktet for forløbene er konstruktivismen som teoriramme. Denne tager udgangspunkt i de enkelte elever og hvordan de lærer, men er i sig selv ikke en arbejdsmetode. Konstruktivismen danner i midlertidigt en konstruktionsramme, hvilken jeg har brugt som grundlag under udvikling af de aktivitetsbaserede udeundervisningsforløb. Ud fra denne tanke skulle den aktivitetsbaserede udeundervisning gerne fordre:
-
en åben opgavestruktur hvor initiativ, aktivitet, problemløsning, eksperimentring, det virkelighedsnære, mening og medansvar er i fokus.
-
at eleverne bliver aktive medspillere og dermed engagerede og motiverede.
-
en induktiv tilgang til arbejdet.
-
at elevernes arbejde bliver centralt og bærende.
-
en proces der udfordrer og benytter begge hjernehalvdele.
-
at eleverne danner sig nye erfaringer på baggrund af arbejdet med projektet.


