Kystmatematik

Kort om forløbet
Danmarks kyster er spændende for børn og unge. De bruger kysten i fritiden, når de bader ved stranden, går tur med forældrene eller fisker og sejler. Kysten er et varieret og spændende naturområde. Kystens kulturhistorie er præget af danskernes tætte tilhørsforhold til havet og der er mange gode fortællinger knyttet til livet langs kysten - fortællinger om fiskeri, sejlads, sørøvere, stormflod, bådebyggere og badeferier.
Formål
Matematikundervisning i de ældste klasser kan foregå andre steder end i klasselokalet. Ved kysten er der mulighed for at inddrage omgivelserne i det matematiske undersøgelsesarbejde. En kyst er under stadig forandring og udgør et levende og alsidigt miljø. Naturens elementer kan være genstand for undersøgelser af vandstanden, kystlinjen eller afstande til øer og klintens top. Også de menneskeskabte havne, badebroer og beplantninger kan bruges og beskrives i matematikundervisningen.
Undersøgelser kan danne grundlag for matematisk modellering og dække flere faglige områder: geometri, tal og algebra og statistik.

Forberedelse
Generel forberedelse
Der er i princippet adgang til alle Danmarks kyster. Det er dog vigtigt at sikre sig at man må opholde sig i længere tid på det kystområde, som er udgangspunktet for undervisningen. Der skal være mere end 50 m til det nærmeste hus og på nogle havne og badebroer skal ejerens tilladelse indhentes.
Husk også at vandstanden kan ændre sig i forhold til vejr og tidevand. Vandet lokker, så det er også en god idé at have styr på skolens baderegler og elevernes badetøj.
Faglig forberedelse
De forskellige aktiviteter lægger op til forskellig forberedelse. Til nogle af aktiviteterne er det er en fordel at forberede eleverne på det faglige stof. Det kan udendørs være svært at forklare hvordan måleudstyr bruges, uddybe begrundelser for formler eller beskrive konkrete regnemetoder. Da der ved kysten ofte er vind og vand er det uheldigt at være meget afhængig af lange forklaringer på kopiark. Evt. kan de vigtigste formler og regnemetoder vises på laminerede ark.
Nogle aktiviteter skal dokumenteres via data, som skal anvendes tilbage i klasselokalet. Resultaterne kan noteres på papir (f.eks. en skov-notesbog) eller indtales eller fotograferes på mobilen. Forbered i klassen metoden til dataopsamling med eleverne, så I er sikre på at få alle relevante data med hjem.
Efterbehandling i klasselokalet
De opgaver, som skal bearbejdes videre hjemme i klasselokalet, kræver at eleverne har præcise data og kan huske det som foregik ved kysten. Igen er et kamera en stor hjælp til at huske og dokumentere arbejdsproces.
Efterbehandlingen skal sikre sammenhængen mellem undervisningen i uderummet og indeundervisningen. I klasselokalet er det oplagt at arbejde med opgaven ved at bruge repræsentationsformer på papir eller computer. Fortællinger, fotoreportager og videoklip kan supplere, hvis resultaterne skal præsenteres for andre.

Sådan gør du
Kom i gang
- Bind for øjnene – stil jer efter højde
- Slå smut – hvem får flest? Er der en form og vægt på den perfekte slå-smut-sten?
- Afsæt en strækning i vandet og lav en svømmekonkurrence. Lad eleverne udforme reglerne.
- Vinkel-leg. Sørg for at der er meget plads og ingen genstande som eleverne kan falde over. I grupper tre og tre. Legen begynder med at de to ”robotter” står med ryggen til hinanden med armene strakt ud og bind for øjnene. Den tredje i gruppen skal få robotterne til at mødes med hænderne mod hinanden. De begynder at gå langsomt i konstant tempo. En dirigerer ved at røre de to andre på skulderen – højre skulder – drej 90 grader til højre, venstre skulder – drej 90 grader til venstre. Legen repeterer forståelse for ret vinkel, er underholdende og giver varmen.
- Gæt 50 m – brug et kropsmål og øv jer i at bedømme afstanden. Kan bruges som indledning til aktivitet 3.
- Find vej på kort. To sidder med ryggen til hinanden. De har samme kort – beskriv en vejstrækning ved at bruge matematikudtryk. Kortet kan være printet fra Google Maps. Husk målestoksforhold.

Aktivitet 1. Stensøjler
Tid
1 time
- en kyststrækning med mange sten
- metermål
- kamera

Aktivitet 2. Hvordan ser din drømmestrand ud?
Tid
1 – 2 timer
- en eller flere forskellige kyststrækninger, gerne med varieret udseende og med badebroer
- målebånd
- målepind til at måle vanddybder
- spande og små skovle
- Vanddybde – beskriv hvordan vandet skal blive dybere fra strandkanten og længere ud. Vurder fordele og ulemper ved lavt og dybt vand. Svømmefærdigheder, vandets temperatur og mulighed for hovedspring.
- Badebroen – længde og form og vanddybde langs broen.
- Sand, sten, græs, skov – hvordan skal naturen være?
- Afstand til toiletter og andre faciliteter.
- Placering i forhold til verdenshjørner. Tænk på vind, bølgehøjder og solen.
- Beskriv målestoksforholdet mellem modellen og den virkelige drømmestrand

Aktivitet 3. Badeforbud?
Tid
1- 2 timer
- En varieret kyststrækning med huse, havne og forskellig vegetation.
- At have øvet jer i at vurdere en afstand på 50 m
- Viden om at vurdere alderen på huse – fra før eller efter 1916
- Kort over kyststrækningen, evt. fra Google maps
- Hvis undersøgelsen inddrager en havn, kan I lave en aftale med havnefogeden om at begrunde badeforbud på havneområdet.
- Naturbeskyttelsesloven (se boks)
|
NATURBESKYTTELSESLOVEN
§ 22. Strandbredder og andre kyststrækninger mellem daglig lavvandslinje og den sammenhængende landvegetation er åbne for færdsel til fods, kortvarigt ophold og badning. Adgang sker på eget ansvar. Det er tilladt kortvarigt at have en båd uden motor liggende på strandbredden. I perioden 1. april-30. september skal hunde føres i snor. Stk. 2. Reglen i stk. 1 omfatter ikke arealer, der inden den 1. januar 1916 er udlagt som have eller inddraget under en erhvervsvirksomhed, der drives på ejendommen. Det samme gælder forsvarsanlæg og havneanlæg. Stk. 3. Offentlighedens adgang må ikke forhindres eller vanskeliggøres. Stk. 4. På privatejede strandbredder og kyststrækninger må ophold og badning ikke finde sted inden for 50 m fra beboelsesbygninger. |
- At vurdere om loven er rimelig
- At undersøge hjemme hvordan loven er besluttet
- At udforme elevernes ”lov”, rimelige regler om hvor man må bade ved danske kyster.
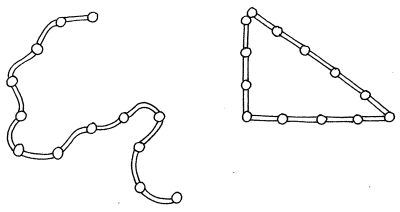
Aktivitet 4. Danmarks kystlinje
|
FAKTA OM ØRIGET DANMARK
Danmark er et ørige med en kystlinie på 8593 km. Danmarks areal er på 43.093 km² og landet består af halvøen Jylland og 406 øer, hvoraf knap en femtedel er beboede. De største øer er Sjælland, hvor hovedstaden København ligger, og Fyn, der har broforbindelse til både Jylland og Sjælland. Danmark er et af Europas mest udprægede øriger, med en samlet kystlinie på 8593 km. Nordsøen afgrænser Danmark mod vest, mens øerne mod øst skiller Østersøen fra Kattegat. De danske øer ligger således på sejlruten fra Østersøen til verdenshavene og samtidig på trafikvejen fra de nordiske lande til Centraleuropa. Denne centrale placering i det baltiske område forklarer, hvorfor landet tidligt udviklede sig til en af Europas betydelige handelsnationer.
Den 69 km. lange landegrænse mod Tyskland i Sønderjylland er landets eneste. Dog blev Danmark fra den 1. juli 2000 også fast forbundet med Sverige via den knap 16 km. lange Øresundsforbindelse mellem København og Malmø.
|
- En kyst (!)
- Et langt reb (100 m) eller flere lange målebånd
- Et stykke fra vandlinjen udmåler eleverne en afstand på 100 m i fugleflugtslinje. Eleverne gætter hvor lang den tilsvarende vandlinje er. Vandlinjen måles efter at eleverne har besluttet en målemetode.
- Der lægges sten i vandkanten med en meters mellemrum over en strækning, som kan genkendes på et kort. Eleverne vurderer om denne målemetode kan bruges til opmåling af kystlinjen
- Vandlinjen skridtes af ved almindelig gang. Der sammenlignes med en given afstand i fugleflugtslinje fra et detaljeret kort.
- Husk at skylle målebånd og reb.
- I kan kontakte Kort og Matrikelstyrelsen (www.kms.dk) og få deres bud på Danmarks kystlinjes længde.
- Kan kystlinjen måles på et kort? Prøv at måle på kort med forskellig målestok.
- Hvem har interesse i at kende kystlinjens længde? (se f.eks. http://komud.dk/danmark-rundt-i-kajak/ )
- Fraktaler og kystlinjer – se faktaboks ”Englands kystlinje”
|
ENGLANDS UENDELIGE KYSTLINJE
For at forstå ovenstående må vi gribe tilbage i tiden. I 1967 havde Mandelbrot i en epokegørende artikel i magasinet Science stillet spørgsmålet: "How long is the Coastline of Britain?". Spørgsmålet kan synes banalt i første omgang: Man kan vel bare finde et kort og måle det op! Mandelbrots pointe var imidlertid, at hvis man tager et kort med mindre målestoksforhold, altså zoomer ind på kystlinjen, så vil det, der på det forrige kort så ud til at være et forholdsvist lige stykker kystlinje, vise sig at at være krogede og bugtede kurver, med en væsentligt større længde end på det forrige kort. Sådan kunne man fortsætte med at zoome ind og få en stadig større kystlinjelængde som følge, Man kan selvfølgelig fremdrage, at denne zoomen ind må stoppe på et tidspunkt, nå man når ned til det atomare niveau eller lignende, men fra et matematisk synspunkt kan forfiningen fortsættes uendeligt.
Eftersom følgen af kystlinjelængder vokser uden begrænsning med graden af zoom, følger det, at der ikke er nogen præcis matematisk definition af længden af en kystlinje.
|
Aktivitet 5. Mål afstanden til en ø, en havmølle, et skib eller enden af molen
- Pinde/pæle, 4 pinde mærket A, B, C og D til hver gruppe. Ekstra pinde medbringes.
- Snor
- Målebånd
- 3 – 4 – 5 snor til rette vinkler
- Lommeregner/mobil
|
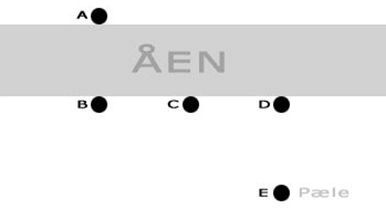
HVOR BRED ER ÅEN ?
|
- Hvis eleverne er uøvede i arbejdet med landmåling kan det være en fordel at prøve at afsætte en ret linje med tre pæle. Eller afsætte et rektangel og lære at afsætte rette vinkler med 3 – 4 – 5 snoren.
- Bed eleverne gætte på afstanden til det, som skal måles. Tal om at vurdere afstande ved at kigge på genkendelige figurers størrelse – huse, master, biler, ol.
- Vis med pinde princippet ved afstandsmålingen. Gør det i lille målestok, så det er nemt at overskue for eleverne (se boks ovenfor og nedenfor).
- Lær eleverne at bruge 3 – 4 – 5 snoren til den rette vinkel. Den følger princippet for Pythagoras sætning: C2 = A2 + B2
- Vær opmærksomme på om eleverne er nøjagtige ved pejlingen.
- Find et relevant forhold mellem den store trekant ud til øen og den ensdannede lille trekant på stranden.
- Udregn via målestoksforholdet mellem de to ligedannede trekanter (se nedenfor).

- Først sætter i en pind A på stranden nogle meter fra vandkanten.
- I vælger et pejlingspunkt P på det, som I vil måle afstanden til.
- Nu skal I tegne en pejlingslinje fra pinden A til vandkanten
- Pinden B sættes 10 – 20 m fra A. Der skal være en ret vinkel mellem pejlingslinjen og linjestykket AB
- I forlængelse af AB afsættes pinden C. Ved målinger til ting som er meget langt væk sættes C 1 meter fra B. Ved afstandsmåling til ting som er tæt ved stranden kan pinden C sættes længere væk fra B.
- Nu går I vinkelret ud fra C, indtil vi kan se pejlepunktet P på båden eller øen gennem pinden i B. Her sætter vi pinden D.
- Afstanden mellem C og D måles.
- Afstanden til P udregnes.
- Check afstandene ved at måle på kort. Diskuter årsager til afvigelser.
- Mål via Google earth
- Eleverne kan bruge også deres viden om ensdannede trekanter til at måle højden af træer, bygninger eller flagstænger.
Baggrund
Vejledning om 300 m strandbeskyttelses- og klitfredningszone
http://www.mitvadehav.dk/media/8899/vadehavsmatematik.pdf - undervisningsideer fra ”På tur med matematikken” - Danmarks Matematiklærerforening
Se spændende fortælling og undervisningsideer under ” Hjelmepiger og sømdrenge”
http://www.kystcentret.dk/ - se undervisningsmaterialer til andre fag