Find vægten

Kort om forløbet

Vi har alle sammen prøvet at blive målt og vejet hos lægen. Men hvad gjorde man i gamle dage, da man ikke havde badevægte? Her er en nem måde at finde ud af, hvor meget en ting eller et menneske vejer – uden vægt.
 

Formål

• Forståelse af kraftens moment.
• Forståelse for betydningen af kraners ballast.
• Forståelse af vægtstangsprincippet.
   

Forberedelse

Det vil være hensigtsmæssigt hvis eleverne har læst om vægtstangsprincippet i en lærebog. En anden mulighed vil være, hvis eleverne går på nettet og læser om Newtons love, og de finder ud af, hvad et kraftmoment er.
 

Sådan gør du

Nedenstående er skrevet til eleverne.

Mål vægt – uden vægt
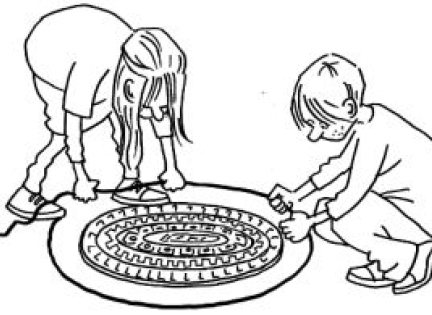
Gå ud at finde en vippe på en nærliggende legeplads. I kan også selv lave en vippe af et stærkt bræt og en trætrille. Du skal huske at medbringe 4 flasker med vand (2 liters flasker).

Vægt i balance
Først skal du få vægten til at balancere, så begge sider vejer lige meget. Det kalder man at kalibrere vægten. Det gør du ved at lægge en vandflaske på vægten, så vippens bræt er vandret (balancerer). Bind flasken fast.

Vej en ven
Herefter skal du finde en tung ting – det kunne f.eks. være en klassekammerat – som du vil måle vægten på. Bind de 3 flasker fast helt ude ved enden af den ene halvdel af vippen, som vist på tegningen. Placer derefter din klassekammerat på den anden side af vippen, så der opstår ligevægt. Det kan ske, at klassekammeraten kommer til at stå meget tæt på midten af vippen (Se tegning).

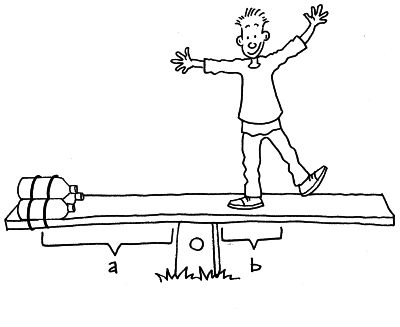
Beregn vægten
Nu skal du prøve at beregne, hvor meget din klassekammerat vejer:

• Du kender allerede til vægten af de tre vandflasker, som vi kalder lille v. Denne vægt er 3 x 2 kg= 6 kg, da 1 liter vand vejer 1 kg.
• For at finde vægten af din klassekammerat – som vi kalder for V – skal du anbringe ham/hende på den anden del af vippen – ret tæt på vippepunktet.
• Dernæst skal du måle afstanden fra lille v til midten af vippen, og fra store V til midten af vippen. Kald den ene afstand ”a” og den anden for ”b”.

Du skal nu stille en ligning op:

a x v = b x V eller V= a x v/b

Ex:
Lad os sige at v er 6 kg, at a er 2 m, og at b er 0,2 m.

Du kan nu regne store V ud ved at sige:

V= 2 x 6/0,2

V= 60 kg

Søjlediagram
Når du har fundet en værdi for vægten V, tegner du den ind i et søjlediagram. Prøv med flere
kammerater og tegn et histogram over, hvor mange kammerater der er i forskellige vægtgrupper.

Baggrund

Vægtstangsprincippet
En vægtstang er et meget enkelt, men effektivt, hjælpemiddel, som I dagligdagen f.eks. bruges til kraners løft (ses ofte ved byggepladser).

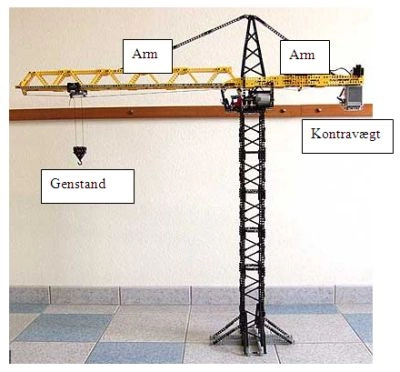
Der er altid balance i kranen, fordi kontravægten kan bevæge sig ind og ud, alt efter, hvor tung genstanden den skal løfte er. Vi kan bruge følgende formel til at udtrykke balancen:
(Genstandens vægt) x lang arm = (kontravægt) x kort arm

Formlen siger, at der er balance, fordi kraftmomentet (dvs. kraft x arm) er lige stort på begge sider af kranen. Formlen er definitionen på vægtsstangsprincippet.

Hammer og sækkevogn
Vægtstangsprincippet bruges mange steder. Når du trækker et søm ud med en hammer udnytter du vægtstangsprincippet.
Når landmanden løfter tunge sække op med en sækkevogn, udnytter han vægtstangsprincippet.
Tænk selv på flere steder, hvor vægtstangsprincippet udnyttes i vores dagligdag.